Building a circuit programmatically

class qucat.Network(netlist)

Constructs a Qcircuit object from a list of components without resorting to a graphical user interface.

The list can be composed of instances of the qucat.L, qucat.C, qucat.R or qucat.J classes for inductors, capacitors, resistors or junctions respectively.

This Qcircuit construction method offers the advantage of programmatically constructing the circuit of the GUI class. On could, for example, construct an array of LC-resonators using a python for loop, which would be tedious using a graphical user interface. The disadvantage is that one cannot use the plotting tools show() or show_normal_modes() to visualize the circuit or its innerworkings.

Parameters:

netlist (list of qucat.Component) – See examples

Returns:

A Qcircuit object, see qucat.Qcircuit

Return type:

qucat.Qcircuit

Examples

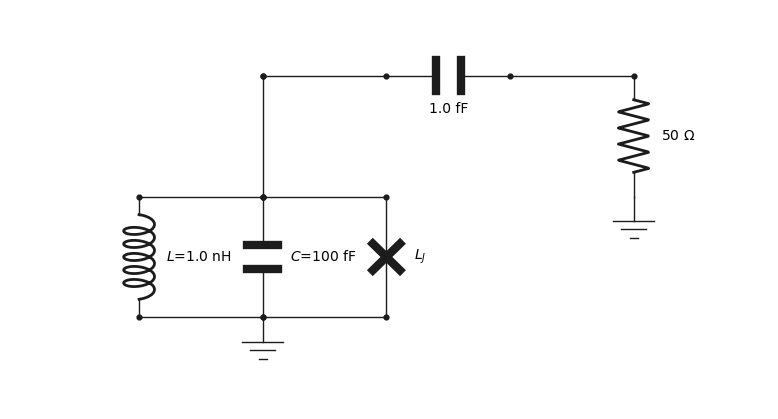
Here we construct a parallel combination of a capacitor, inductor and junction, grounded on one end and connected at the other end through a capacitor to a 50 Ohm resistor to ground.

Import the Network class, and the components we will need

>>> from qucat import Network, R,L,C,J

Note that the components (R,L,C,J) accept node indexes as their two first arguments, here we will use the node 0 to designate ground. The last arguments should be a label (str) or a value (float) or both, the order in which these arguments are provided are unimportant.

>>> circuit = Network([
... L(0,1,'L',1e-9), # Add the inductor between ground and node 1
... C(0,1,100e-15,'C'), # Add the capacitor
... J(0,1,'L_J'), # Add the junction
... C(1,2,1e-15), # Add a capacitor which will connect to a resistor
... R(2,0,50) # Add a 50 Ohm resistance to ground
... ])

The junction was parametrized only by a string L_J , this is the best way to proceed if one wants to sweep the value of a component. Indeed, the most computationally expensive part of the analysis is performed upon initializing the Network, subsequently changing the value of a component and re-calculating a quantity such as the frequency or anharmonicity can be performed much faster.

For example, we can compute the eigenfrequency, loss-rates, anharmonicity, and Kerr parameters of the circuit for a specific junction inductance.

>>> circuit.f_k_A_chi(L_J = 1e-9)